Il principio del minimo sforzo

"Poiché a chiunque ha, sarà dato
e sarà nell'abbondanza.
Ma a chi non ha, sarà tolto
anche quello che ha"
(Matteo 25, 29)

George Kingsley Zipf (1902-1950) non era un matematico ma un filologo e linguista americano ma grazie alla sua scoperta, suo malgrado, divenne anche lui un Cacciatore di numeri. Dopo aver intrapreso la carriera accademica come docente ad Harvard indirizzò i suoi studi in un settore da lui stesso denominato: “Ecologia umana statistica”.

Nel suo percorso di studio fu particolarmente influenzato dalle conclusioni a cui giunse l’economista italiano Vilfredo Pareto sulla “naturale” tendenza a concentrare la distribuzione della ricchezza nelle mani di una ristretta cerchia elitaria, queste osservazioni sulle classi sociali divennero poi note come “Principio di Pareto”.

Zipf volle verificare tale regola distributiva anche in campo linguistico, quindi, iniziò un lungo e paziente lavoro di classificazione conteggiando la distribuzione di frequenza delle parole presenti nei più noti testi classici della letteratura, scoprendo che in tutti i testi, indipendentemente dalla lingua usata, tra la parola più frequente e le altre parole ordinate in ordine decrescente esiste sempre una relazione inversamente proporzionale che lega la frequenza di apparizione delle singole parole alla loro posizione (rango). Per cui se, per esempio, la prima parola più frequente nel testo appare 1000 volte la decima avrà una frequenza approssimativamente pari a 100.

Zipf aveva scoperto empiricamente uno schema linguistico universale applicabile, con sfumature diverse, ad ogni forma di scrittura evoluta, e che può essere riassunto in questa elementare equazione: Fp = C / n’.

Ove: Fp = la frequenza delle parole presenti nel testo, n = il posto (rango) che occupano in una lista in cui sono sistemate in ordine decrescente di frequenza; il valore n viene elevato ad un esponente (‘) prossimo a 1, che può variare in base alla lingua ma che si avvicina circa a 1,04. Quindi, nel linguaggio umano emerge una “legge” di potenza che governa la scrittura. Per effetto di questa “proprietà” intrinseca del linguaggio umano, tra le parole appaiano profonde diseguaglianze, alcune  apparivano molto frequentemente, altre molto meno (e fino a qui potrebbe quasi essere un’ovvia considerazione), ma l’aspetto straordinario fu che la diseguale distribuzione segue una precisa sequenza distributiva.

Zipf incominciò a riflettere sulle cause di questo fenomeno ponendosi sostanzialmente la seguente domanda: per quale motivo i testi scritti in lingue diverse e da autori diversi seguivano tutti la stessa relazione distributiva delle parole? Non poteva che sussistere un qualche schema matematico che governa il linguaggio umano. Il tratto caratteristico di questo schema è quello di ottimizzare l’uso delle parole in quanto si riscontra che le parole più usate sono prevalentemente i termini più brevi, più semplici e veloci da scrivere e pronunciare, quasi che vi fosse un criterio di economicità nella scelta delle parole, così da rendere minimo lo “sforzo” per la costruzione del testo e questo per tutte le lingue del mondo.

La grandezza di Zipf fu quella di uscire dal contesto linguistico, scoprendo che questa proprietà non era solo limitata al mondo letterario, ma che si potesse estendere a molte altre attività umane, sociali ed economiche ed addirittura ai fenomeni naturali.

Questa caratteristica prende oggi il nome di Legge di Zipf definita dal “Centro Ricerche ENRICO FERMI” di Roma come una: Regolarità statistica ubiqua nei sistemi complessi.

 

Al di fuori dell’ambito linguistico

Un esempio in campo demografico è il seguente: considerando le principali città di una nazione, tale legge sostiene che la popolazione della seconda città più popolosa all’interno di uno stato è circa pari alla metà della prima, la terza sarà circa un terzo, la quarta sarà circa un quarto, e così via. Questo andamento caratterizza infatti, a grandi linee, anche la popolazione delle città italiane classificate in milioni (M) di abitanti:

1. Roma 2.84 M la prima città italiana, punto di riferimento
2. Milano 1.40 M (circa ½ di 2,84)
3. Napoli 0.90 M (circa 1/3 di 2,84 )
4. Palermo 0,65 M (circa ¼ di 2,84)
5. Genova 0,57 M (circa 1/5 di 2,84)
6. Bologna 0,40 M (circa 1/6 di 2,84)  ecc.

Naturalmente, la popolazione delle città è un fenomeno del tutto diverso da quello del linguaggio, ma entrambe sono “governate” dallo stesso principio quello che conduce il fenomeno alla massima efficienza e parsimonia ovvero: “Il Principio del minimo sforzo”, come lo definì Zipf stesso. Le persone trovano che, in genere, è più vantaggioso andare ad accrescere la popolazione delle città di maggiore dimensione piuttosto che nei centri minori, poiché vi sono maggiori “utilità” (nel lavoro, nei rapporti sociali ecc..) nel vivere nelle grandi città di gran lunga superiori rispetto allo “sforzo” necessario per abitarci. Abbiamo quindi, (poche) città “ricche” di abitanti ed altre (molte) che sono assai più “povere” di cittadini. Non vi è una città tipica media in cui si avvicinano la maggior parte delle città. Pochi insediamenti urbani prendono tutto il grosso degli abitanti, ai più piccoli spettano solo le briciole.

                                                                                                                                                                                    La prima diseguaglianza nelle relazioni sociali, per ora solo demografica trova riscontro nella Legge di Zipf.

 

Le leggi di potenza: il modello della disuguaglianza

Già tra la fine dell’800 e l’inizio del ‘900 alcuni studiosi si resero conto che molte variabili mostravano caratteristiche diverse da quelle spiegate dalla distribuzione normale, soprattutto perché presentavano livelli di “disuguaglianza” molto marcati.

L’esempio più celebre, come già ricordato, è quello di Vilfredo Pareto che alla fine dell’800 aveva constatato come in Italia il 20% della popolazione fosse proprietaria dell’80% delle terre. La regola di Pareto o dell’80/20 fu poi immediatamente applicata alla distribuzione della ricchezza. Ma fu solo Zipf che negli ’30 comprese l’universalità di questo Principio che fu poi illustrato dal testo pubblicato da Zipf nel ’49, un anno primo della sua scomparsa: “Il comportamento umano: Il Principio del minimo sforzo”.

La ricchezza il linguaggio, gli abitanti delle città e molti altri fenomeni seguono una distribuzione molto diversa da quella che in statistica è definita di tipo “normale” (ove i dati si addensano in modo simmetrico intorno al loro valore medio) tale distribuzione viene definita “legge di potenza” (in quanto le sue caratteristiche matematiche sono definite da una funzione esponenziale).

Di seguito un esempio grafico della distribuzione della ricchezza secondo una legge di potenza:

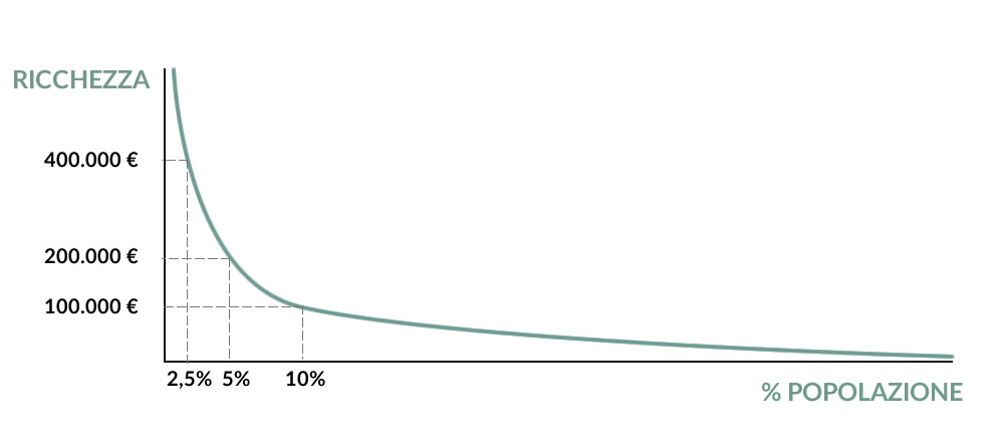
Esempio di legge di potenza della ricchezza (esponente 1). Dati puramente indicativi.

Nel grafico si ipotizza che il 10% della popolazione abbia un patrimonio superiore a € 100.000, il 5% un patrimonio superiore a € 200.000, il 2,5% superiore a € 400.000 e così via crescendo in maniera esponenziale. Come evidente dal grafico le leggi di potenza sono caratterizzate da un livello di disuguaglianza molto pronunciato: gli eventi estremi sono decisamente più probabili rispetto alle distribuzioni “normali”. Un numero limitato di persone ha patrimoni molto grandi mentre la stragrande maggioranza degli individui ha patrimoni limitati.

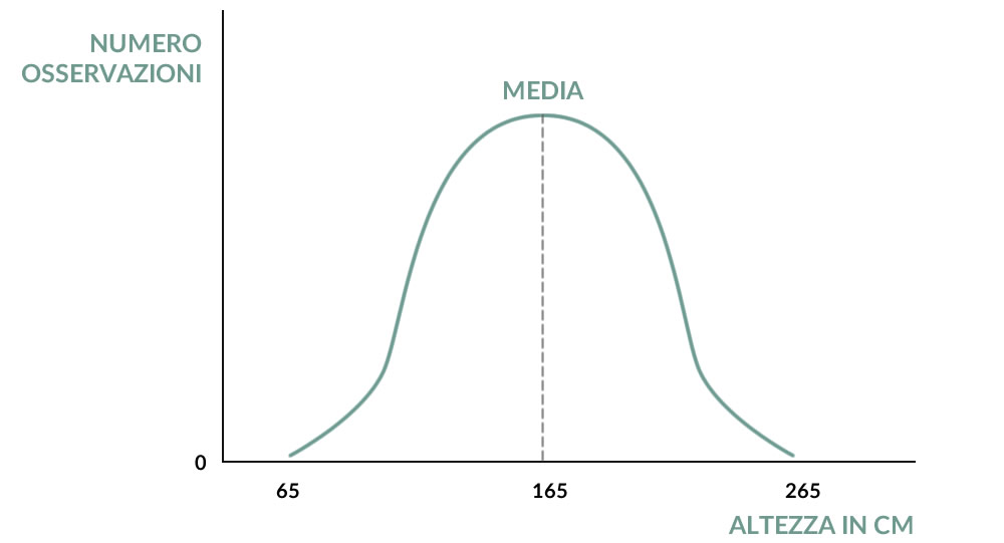
Diversamente dalla ricchezza l’altezza delle persone invece segue una distribuzione “normale” in cui trionfa una sostanziale eguaglianza. Se l’altezza degli esseri umani fosse dominata dalle leggi di potenza avremmo un mondo abitato da molti nani e un ristretto numero di giganti. Le caratteristiche di vari fenomeni sono descritte attraverso un modello statistico definito “distribuzione a campana”. Nella figura di seguito riportata trovate un esempio della distribuzione dell’altezza negli individui in età adulta.

Distribuzione “normale” a campana dell’altezza degli individui adulti:

Assai più numerosi sono i fenomeni caratterizzati da distribuzioni non normali e da forti ineguaglianze come abbiamo visto la ricchezza, il linguaggio, le popolazioni delle città sono eventi caratterizzati da Leggi di Potenza ma anche

le vendite di libri e gli streaming musicali,

i “click” sui siti internet,

la capitalizzazione delle società quotate in borsa,

i danni causati da terremoti e altre calamità naturali,

le vittime delle guerre,

la volatilità del mercato azionario e potremmo continuare ancora a lungo.

I fenomeni governati da leggi di potenza, hanno una netta inclinazione ad amplificare i fenomeni estremi le medie aritmetiche non rappresentano la normalità; media e mediana divergono profondamente tra loro, sono il regno delle diseguaglianze.

Zipf spiega la diffusione del suo Principio in ambito socio-economico nella irrefrenabile tendenza dei comportamenti umani a raggiungere i risultati con la produzione del minimo sforzo, questa condizione avvantaggia alcuni pochi operatori economici che riescono ad accaparrarsi velocemente quote di mercato a scapito della gran parte degli altri e questa posizione dominante tende a rafforzarsi.

Una grossa piattaforma di commercio elettronico assolve in pieno il desiderio di limitare gli sforzi economici, logistici e fisici dei consumatori che si trovano a soddisfare i loro desideri con poca spesa e l’impareggiabile comodità di ricevere il loro acquisto a domicilio in qualunque ora del giorno, un vero trionfo dell’efficienza si potrebbe dire, ma anche il presupposto di future diseguaglianze e immense concentrazioni di ricchezze.

I moderni mercati finanziari sono il contesto in cui si sono manifestati più spesso gli effetti delle leggi di potenza. Infatti, sono sistemi indubbiamente complessi soggetti a violente repentine oscillazioni molte volte inspiegabili, hanno prodotto immense ricchezze concentrate nelle mani di una ristretta oligarchia finanziaria. La favola neo-liberista dei mercati efficienti che trova la sua teorizzazione nel cosiddetto “random walk” il percorso causale dei mercati in cui nessun operatore può trarre vantaggi di posizione a danno di altri sulla base del fatto che il prezzo degli strumenti finanziari (azioni, fondi ecc…) sconta tutte le informazioni note a tutti, sia quelle attuali, sia soprattutto quelle attese. In base a queste assunzioni i mercati finanziari si muovono nel tempo assumendo una distribuzione “normale” intorno al valore medio di lungo periodo, per cui dovrebbero essere un luogo tranquillo in cui gli eventi estremi rappresentano casi eccezionali assolutamente improbabili.

Tale assunzione si infrange miseramente sulle osservazioni delle dinamiche finanziarie di questi ultimi decenni, secondo la teoria dei mercati efficienti questi avvenimenti dovevano essere praticamente impossibili. La volatilità avvenuta risulta inspiegabile in una distribuzione dei prezzi “normale” proprio perché tale non è. I mercati che sono sistemi complessi tutt’altro che tranquilli ed estremamente rischiosi in cui dominano leggi di potenza coma la Zipf, producono estremismi ed iniquità. Proprio partendo dalle legge di Zipf a tali conclusioni giungono il grande matematico Mandelbrot padre della Geometria Frattale nel suo libro “Il disordine dei mercati” e il filosofo e matematico grande esperto di finanza Nassim Taleb nel suo famoso libro “Il cigno nero”, a cui dedicherò una prossima pubblicazione in questa rubrica.

 

Conclusioni

Come afferma il Centro di Ricerche Enrico Fermi di Roma:

“Nonostante queste ubiquità e i molteplici tentativi fatti per spiegare l’origine della Legge di Zipf, non è ancora stato individuato un unico meccanismo generativo capace di spiegare tutte le sue manifestazioni…”.

Anche qui, come per la Legge di Benford, sono passati oltre 70 anni ma ancora oggi non riusciamo a comprendere la vera natura di questi “schemi” nascosti che condizionano, nostro malgrado, le nostre esistenze ed il mondo che ci circonda.