La memoria del Nilo

... e dal Fiume ecco salire sette vacche, di bell'aspetto e grasse, che si misero a pascolare nella giuncaia. Dopo quelle, ecco salire dal Fiume altre sette vacche di brutto aspetto e scarne, che si fermarono accanto alle prime, sulla riva del Fiume.

                                                                                    Genesi 41, 2-3

 

Indice

1. L’esponente di Hurst

2. L’applicazione nella Finanza

3. Il modello Browniano

4. Conclusioni

 

 

1. L’esponente di Hurst

Doveva essere molto orgoglioso di sé il giovane ingegnere idraulico Harold Edwin Hurst, figlio di un capomastro di mezzi modesti  aveva avuto  un’ adolescenza travagliata avendo abbandonato gli studi ed andando a lavorare in una falegnameria, però, in seguito, dopo aver frequentato  dei corsi serali,  riuscì a vincere una borsa di studio ad Oxford e con grande sorpresa dei suoi famigliari riuscì a laurearsi a pieni voti. Grazie alla sua brillante carriera arrivò infine ad ottenere, nel 1906, un incarico prestigioso in Egitto, allora facente parte dell’impero britannico. In quegli anni le fabbriche di cotone del nord dell’Inghilterra ,in piena espansione industriale ,reclamavano crescenti  quantità di cotone egiziano, i cui livelli di produzione erano strettamente legati al ciclo delle piene del Nilo.

Il compito affidato al giovane Hurst era tutt’altro che semplice, con il ruolo di direttore scientifico della spedizione doveva fare indagini sul posto al fine di migliorare la capacità di prevedere  le piene del Nilo in modo da ottimizzare le dimensioni delle dighe in costruzione. Il problema delle dighe è che se le si fa troppo basse allora il loro costo è limitato ma negli anni nei quali le piogge sono sopra la media si spreca il prezioso liquido che sarà assente negli anni siccitosi; di converso, se le si fa troppo alte si sprecheranno  i costi di costruzione  di tutta quella parte dell’invaso che rimarrà perennemente all’ asciutto. In merito al Nilo, a dispetto del fatto che da secoli si tenesse memoria scritta sulle inondazioni sembrava che le dighe costruite dagli ingegneri venissero ciclicamente messe fuori uso da piene più imponenti di quanto era logico aspettarsi. Il procedimento utilizzato dagli ingegneri sul Nilo  è il seguente: dapprima si calcola la misura della  cubatura media di acqua in uscita, dal bacino del lago Albert  e si ipotizza che quello sia l’obiettivo in uscita da perseguire con l’aiuto delle dighe , sarebbe infatti non realistico pensare di superare in media quel valore , le piogge non basterebbero ed  il livello del lago Albert finirebbe ad abbassarsi progressivamente cosi come puntare ad un flusso medio futuro inferiore avrebbe portato ad una perdita  d’uso del prezioso liquido e quindi arrivare a ridurre  la produttività delle coltivazioni cotoniere.

Il problema del Nilo era che non si conosceva di quanto potesse straripare il fiume, in pratica era ignota la sua volatilità. Ciò poteva portare a stati di prosperità alternati a stati di povertà piuttosto frequenti per il popolo egizio. Per dare un’idea dell’importanza del fenomeno, la lunghezza del Nilo è pari a 6700 chilometri e solo il suo bacino ricopre il 10% del territorio Africano, la sua portata passa da 151 miliardi di metri cubi a 42 miliardi. L’avventura di Hurst iniziò quando le fabbriche di Manchester, interessate al cotone egiziano come abbiamo sopra menzionato, incaricarono Hurst di realizzare un progetto chiamato “Century Storage”, che aveva lo scopo di accantonare una quantità di acqua necessaria per far fronte alla massima siccità possibile, attraverso un sistema di dighe. Naturalmente questo era un incarico molto difficile da portare a termine perché nessuno aveva idea della grandezza della piena dell’anno successivo, il buon senso (e la logica) avrebbe portato ad ipotizzare che il susseguirsi delle piene sul lungo termine seguisse un percorso del tutto causale.

Come pensare che le piene del passato possano influire sulle future successive precipitazioni? L’intuito ci dice che l’andamento delle precipitazioni segue un percorso casuale (un Random Walk  usando un termine caro alla Finanza anglosassone ) per cui l’evento del passato non influisce su quello  futuro, essi sono tra loro perfettamente indipendenti. Pertanto,  se si volesse costruire una diga basterebbe prendere la deviazione cumulata ottenuta sommando le differenze tra la il flusso d’acqua in metri cubi annuale meno la media aritmetica  della serie storica e costruire un tabella in cui si individua il valore massimo di tale  deviazione cumulata ed il suo valore minimo a questo punto la differenza, in valore assoluto, tra il valore massimo ed il minimo è detto Range e lo indica con R, se il percorso storico delle piene del Nilo fosse del tutto casuale (come ci si aspetterebbe) allora (tenendo conto della volatilità del fenomeno ovvero la dispersione delle variabili rispetto alla loro media aritmetica  misurata dallo scarto quadratico medio:  σ) l’ampiezza massima ,che  si potrebbe immaginare, delle portate d’acqua future per stabilire la dimensione della diga dovrà tenere conto della seguente relazione R =  2N/2 x σ. Per cui  con una più alta volatilità (rischiosità) del fenomeno (misurata da σ) mi aspetto una  crescita dell’ampiezza del fenomeno idrico R maggiore rispetto a quello con una più bassa volatilità il tutto  proporzionato dalla radice quadrata del numero degli anni N diviso 2.

La scelta della radice quadrata è legata all’ipotesi iniziale, ovvero: che la dinamica delle precipitazioni attese siano del tutto casuali  (random walk). Quindi, se si vuole  costruire  una diga che regga alle piene future ma ,al tempo stesso, costare il meno possibile si seguirà un dimensionamento  diverso a seconda del fatto che la diga debba durare N= 50 anni  piuttosto che N = 100 anni.

Tutto risolto allora? No, perché altrimenti non si spiegherebbero gli insuccessi del passato. Hurst capiva che qualcosa non tornava e per dimostrarlo fece un esperimento tanto semplice quanto efficace prese i dati storici annuali delle portate d’acqua e associo ciascuno di questo valore ad una carta di un mazzo di carte da gioco e dopo averlo mischiato ricostruì  la serie di dati in modo del tutto nuovo e casuale (aveva di fatto randomizzato i dati) media aritmetica e la deviazione standard (σ) ovviamente, non cambiavano e se il percorso della serie storica  fosse stato casuale non avrebbe portato  alcuna influenza sul risultato di R mettere o meno in successione storica i dati. Hurst rifece tutti i calcoli e si accorse che randomizzando i dati storici, il valore di R era decisamente più basso rispetto a quello effettivamente misurato. Seguendo il criterio della indipendenza tra le precipitazioni del passato su quelle del futuro, si avrebbe dato seguito ad  un dimensionamento della diga più contenuto  rispetto al dovuto e quindi si sarebbero assunti inconsapevolmente rischi maggiori di quelli  attesi.

In realtà il percorso non è casuale, come se ci fosse una sorta di dipendenza con le variazioni passate, il fiume quindi ha una “memoria di lungo periodo” (Long Range Memory) era come se le piene del passato rafforzassero anche quelle future e dopo l’inversione del ciclo i periodi siccitosi, a loro volta, rafforzassero quelli futuri.

Possibile? Vi era uno “schema" nascosto nei cicli idrografici? Hurst, che al pari di Benford e Zipf era un “cacciatore di numeri" (si vedano i miei precedenti articoli) che non si fermava alle apparenze o alle convinzioni dominanti si rese conto che questa “stranezza" non si limitava al flusso d’acqua del Nilo ma aveva una portata generale. Infatti, studiò svariati fenomeni naturali prima di arrivare ad elaborare una regola universale: le misure delle precipitazioni da Adelaide a Washington D.C., i valori della temperatura da St.Louis a Helsinki, gli anelli dei tronchi dei pini e delle sequoie, le macchie solari ecc. Finalmente arrivò ad una formula generale ed elaborò l’ Esponente di Hurst (H) ovvero una potenza di circa ¾ (più precisamente H = 0,73 da applicare alla radice): in natura i percorsi non erano casuali.

Infine arrivò a scrivere una formula modificata:

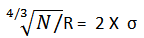
L’Ampiezza massima attesa futura della portata delle acque diventa maggiore rispetto a quella misurata con l’ipotesi del Random Walk e ciò è tanto più vero in presenza di un volatilità (espressione di rischiosità) misurata da un σ crescente.

 

2. L’applicazione nella Finanza

Abbandoniamo le “bibliche “ acque del Nilo per ricondurre la scoperta di Hurst ai Mercati Finanziari e ai danni che gli stessi possono portare all’economia reale.

Fu il grande matematico Benoit  Mandelbrot, padre della “geometria frattale” a cui rinvio nel suo libro: Il Disordine dei Mercati – Edizione Einaudi ad estendere l’applicazione dell’ “Esponente di Hurst”  ai mercati finanziari, impostando una semplice proporzione: le piene stanno ai grandi balzi dei prezzi come le siccità ai crolli di mercato.

Mandelbrot aveva constatato evidenti correlazioni tra i prezzi passati e i prezzi successivi del cotone, elaborando anche per i mercati finanziari il concetto di dipendenza a lungo termine. Secondo questa teoria, qualsiasi atto compiuto nel mercato non è privo di conseguenze; essendo un sistema dinamico il risultato di qualsiasi processo è sensibile al punto di partenza (effetto farfalla). Aziende, tassi di cambio, indicatori macroeconomici, commodity ecc. sono tutti collegati in qualche misura, però non è possibile per noi comprenderli. Mentre il concetto di base era che le variazioni di prezzo dal tempo iniziale al tempo finale fossero indipendenti e presupponessero un coefficiente di Hurst pari a ½ (radice quadrata) , secondo Mandelbrot esiste una sorta di memoria a lungo termine e quindi è probabile che il coefficiente abbia un valore maggiore di ½. Facendo un esempio: se i tassi di cambio hanno una dipendenza a lungo termine, l’aumento dei tassi tenderà a continuare anche il giorno successivo e ancora, fino ad allontanarsi definitivamente dal punto di partenza. Ipotizzare che il coefficiente (H) sia pari a 0,5 implica che non esista una dipendenza tra i dati della serie storica. Un H pari a 0,9 indica movimenti di prezzi persistenti, che seguono una tendenza (ovviamente questo non vuol dire che si muovano in una -sola direzione il ciclo, prima o poi,  cambierà certamente verso ma dopo aver esaurito la sua “memoria storica") in questi casi per questi strumenti finanziari è efficace l’analisi tecnica nell’individuare trend rialzisti o ribassisti che tenderanno a persistere . Quando invece si osserva un H pari a 0,1  con uno schema a zig zag, ciò implica che la variabile tende a cambiare molto frequentemente direzione i movimenti dei prezzi sono detti: anti-persistenti.

 

3. Il modello Browniano

Il valore di H è ricompreso tra:  0 < H < 1, il modello Browniano presuppone un H pari a 0,5. I modelli finanziari si  basano su questo concetto, mutuato dalle scienze naturali,  scrive Mandelbrot nel sopracitato testo (Il Disordine dei Mercati pag. 179) : “…. Il moto browniano misura il movimento delle singole particelle nell’acqua nel tempo. In questo caso si applica la già citata regola della “radice quadrata": una particella  che si muove per cento secondi si allontanerà dieci volte (radice quadrata di 100) di più di una particella che si muove in un solo secondo. Applicare questa regola ai prezzi dei mercati è molto comodo poiché se ne ricava quanto può variare  il prezzo di un bene e  quali probabilità ha di oscillare nell’ambito di quell’ampio intervallo.

“Seguendo il moto browniano la distribuzione di frequenza del fenomeno osservato andrà a formare la classica curva a “campana” di tipo gaussiano, con una simmetrica ripartizioni delle opposte situazione aventi come baricentro il valore medio che diviene il punto di equilibrio. I fenomeni veramente estremi sono talmente rari da essere considerati in pratica inesistenti. Secondo  le ipotesi sviluppate da Bachelier i prezzi dei mercati finanziari influenzati da una innumerevole quantità di cause seguono una distribuzione gaussiana a campana. I prezzi storici non danno alcun contributo il passato non influenza il presente ne tanto meno il futuro. I mercati alla fine tendono al loro punto di equilibrio e gli eventi estremi non sono  neppure da considerare essendo semplicemente improbabili.

La storia finanziaria ha purtroppo insegnato che questo mondo “idilliaco" teorizzato da Bachelier non esiste i mercati sono intrinsecamente instabili l’equilibrio di lungo periodo un’utopia e gli eventi estremi sono certamente poco frequenti ma accadono e quando ciò avviene le conseguenze sono spesso disastrose la curva distributiva reale non è quella rassicurante a “campana”, ma una curva con una minacciosa “coda lunga”. I teorici del random walk non potranno mai spiegare gli eventi estremi a cui abbiamo assistito in questi ultimi decenni, secondo le loro teorie lo scarto dalla media registrato è talmente ampio da non essere spiegabile. La persistenza in economia e finanza della dottrina dell’equilibrio nonostante le evidenze empiriche avverse è appagante per il sistema “dell’industria finanziaria” che preferisce agire in un ambiente dipinto come tranquillo capace di autoregolarsi  rispondendo agli shock esterni e ricomponendosi  verso il punto di equilibrio, basta lasciare agire le forze del mercato  per il tempo che serve e tutto, alla fine, andrà a posto. Questa visione è perfettamente conforme alle raccomandazioni neo liberiste che sollecitano di lasciare agire  le forze della domanda e dell’offerta astenendosi da qualsiasi ingerenza esterna.

 

4. Conclusioni

Lo spirito di osservazione di Hurst ha svelato che anche il Nilo, nei sui cicli naturali, è governato da una “legge di potenza" per cui gli eventi estremi (piene) possono essere disastrose la memoria a lungo termine del Fiume determina una spinta inerziale che si trascina dal passato e si accumula sul presente potenziando gli effetti.

Anche i mercati finanziari hanno le stesse caratteristiche le loro dinamiche sono governate da leggi di potenza. In conclusione:

1) il sistema finanziario sottostima il rischio reale;

2) di conseguenza anche la remunerazione del rischio, gravante sui risparmiatori è assolutamente sottostimata. Gli strumenti di misura del rischio, costruiti sulla base di un impianto teorico fallace non sono affidabili.

La finanza è  come una nave che si muove verso acque agitate con un barometro di bordo a cui è vietato segnare tempesta.