Legge di Benford: significato, storia ed applicazioni

Tutte le cose dritte mentono.

Ogni verità è ricurva, il tempo stesso è un circolo (

Friedrich Nietzsche)

 

Indice:

1. Premessa

2. Legge di Benford: definizione

3. Cenni Storici

4. Applicazioni della legge di Benford

5. Spiegazione del fenomeno

6. Condizioni applicative e proprietà

7. Come misurare il livello di “conformità” alla Legge di Benford

8. Interpretazione dei risultati con Test Statistici

9. Difficoltà operative

10. Prospettive future

11. Conclusioni

 

1. Premessa

Viviamo in un mondo immerso nei numeri, sia nel contesto privato ma, ancor di più, in quello pubblico allargato della cosiddetta “infosfera”. Le nostre scelte personali e collettive dipendono da una quantità enorme di valori numerici provenienti dalle più disparate fonti, di cui, in prevalenza, non abbiamo alcun controllo, esse però influenzano pesantemente le nostre decisioni. Come possiamo veramente essere sicuri della loro autenticità?

Molte volte affidiamo la loro validazione a Istituzioni, costituite a tale scopo, ma per lo più (soprattutto ora con la diffusione delle informazioni attraverso la Rete Internet) non vi è alcuna forma di verifica, ecco quindi spiegato il diffondersi delle cosiddette fake news. In questo vorticoso contesto informativo un contributo significativo per gettare uno “sguardo di verità” può essere apportato dall’utilizzo “critico” della “Legge di Benford”. Procedo, quindi a definirne i contenuti.

 

2. Legge di Benford: definizione

La definizione moderna di matematica è quella di scienza degli schemi, definizione assai più ampia rispetto a quella tradizionale di scienza dei numeri. In quanto scienza degli schemi oggi la matematica arriva a dedicarsi allo studio di ogni aspetto della natura fisica ed umana. Infatti, si è scoperto che ci sono schemi astratti alla base del pensiero, delle comunicazioni, dei calcoli, della società e persino della vita stessa.

La legge di Benford (altrimenti detta Legge della Prima Cifra) è proprio uno schema universale matematico- statistico che fornisce la frequenza con cui si distribuiscono le singole cifre nelle serie numeriche che, come vedremo, presentano determinate caratteristiche. La distribuzione delle prime cifre a sinistra delle serie numeriche non è equamente ripartita, come direbbe il senso comune, ma tende a conformarsi ad una precisa collocazione con frequenze più alte a partire dalla cifra 1 fino a scendere velocemente alla frequenza più bassa associata al numero 9. Tale distribuzione di frequenza non è limitata solo alla prima cifra ma può essere assegnata anche alle prime due cifre (ovvero da 10 fino a 99) o alle prime tre cifre ecc..

Da un punto di vista matematico tale legge si esprime in sintesi nella seguente relazione logaritmica: (1) B(i) = log (1 + 1/d): ove B(i) è la frequenza, in valore decimale, di apparizione della singola cifra e “d” è la singola cifra. Questa equazione misura la frequenza della prima cifra a sinistra di ciascun numero (che va ovviamente da 1 a 9).

La Legge di Benford, quindi, determina la distribuzione di probabilità con cui misurare la frequenza di collocazione delle singole cifre all’interno dei numeri, appartenenti a serie di dati, espressione quantitativa di diversi fenomeni: naturali, demografici, sociali e quindi anche economico-finanziari e contabili.

Nel caso della prima cifra la distribuzione di frequenza sarà la seguente:

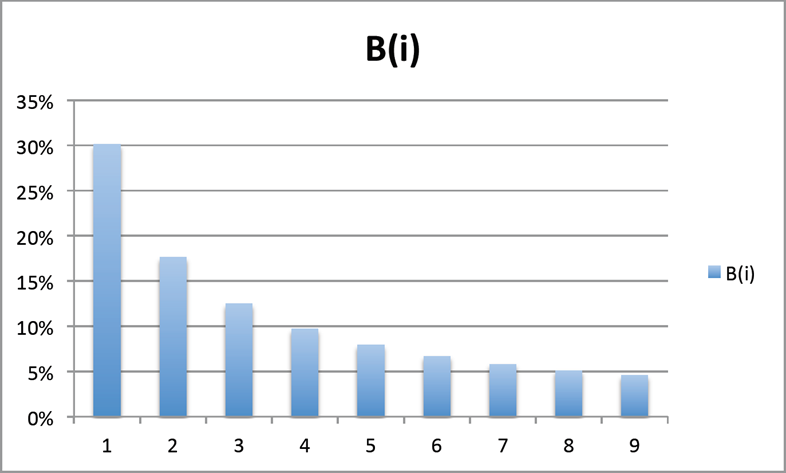
Come si può notare il decadimento della frequenza di apparizione della cifra è molto veloce già a partire dalle cifre 2 e 3, a dimostrazione che si tratta di un processo non lineare, per poi assestarsi verso le cifre 7, 8, 9, che appaiono nei numeri circa sei volte meno della cifra 1.

La sua applicazione non si limita alla prima cifra a sinistra di ciascun numero ma vale per tutte le cifre, singole o tra loro accoppiate, che formano ciascun numero la cui distribuzione di probabilità varia in funzione della collocazione nel numero: più si va verso destra più le cifre tendono ad apparire in modo equidistribuito.

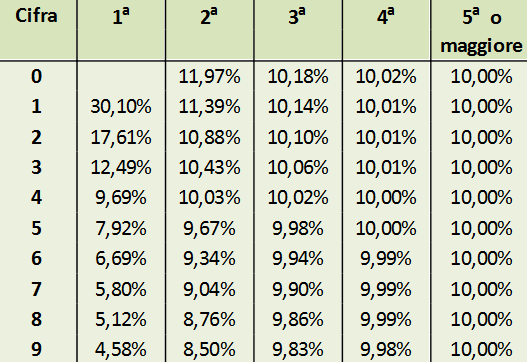
Dalla 4 cifra in poi si arriva alla sostanziale equidistribuzione.

 

3. Cenni Storici

 

Ho classificato la Legge di Benford come uno schema matematico statistico, ma la scoperta di questa affascinante proprietà non è il risultato della geniale intuizione di un brillante matematico ma il frutto del tenace lavoro di ricerca di un fisico, impiegato alla General Electric,  Frank Benford, che negli anni trenta aveva intuito (proseguendo i lavori di una felice constatazione del matematico canadese Newcomb di fine ‘800) che le cifre dei numeri presenti nelle serie storiche prodotte dalla misura dei più disparati fenomeni: naturali, demografici e socio economici non fosse casule, ma che seguisse una ben definita “legge”.

Quindi, fece un lungo studio conteggiando le cifre di serie numeriche estratte da un numero considerevole di diverse fonti statistiche: lunghezza dei fiumi, altezza di montagne, numero di abitanti delle città, movimenti dei conti correnti, ecc… in tutti questi casi le prime cifre concordavano nella distribuzione di frequenza indicata nella sopracitata tabella, che lui chiamò “Legge dei numeri anomali”. La sua ricerca fu pubblicata nel 1938 nella Rivista dell’American Philosophical Society e per molti decenni fu dimenticata.

 

Frank Benford:

Il fatto che tale proprietà non fu individuata da un matematico attraverso lo schema classico: ipotesi, tesi e dimostrazione, bensì fu empiricamente scoperta da un fisico, per di più nell’ambito di una ricerca portata avanti a titolo personale e volontario, la relegarono ai margini del contesto accademico dell’epoca. Assunse il titolo di “legge” in quanto figlia di una constatazione empirica e pertanto non dimostrata con il rigore formale che contraddistingue la matematica classica nei Teoremi

Solo con l’avvento dei primi elaboratori elettronici essa fu riscoperta dalla felice intuizione del prof. Mark Nigrini, che la rese nota al mondo della professione contabile. Finalmente nel 1996 il professor Theodor Hill, attualmente la maggiore autorità scientifica in materia, ne consacrò la piena dignità in campo matematico.

 

4. Applicazioni della legge di Benford

 

Una volta scoperto questo schema universale, chiave di lettura del sistema numerico, abbiamo a disposizione una vera e propria “bussola di verità” e i campi di applicazione hanno come unico limite la fantasia. La legge ha trovato utili applicazioni nel campo scientifico: in fisica, astronomia, geologia, medicina….

Ma anche e soprattutto in campo socio economico: revisione legale e attività forense, in primis, e nelle scienze sociali in vari ambiti, di cui daremo ora solo un breve cenno. Per esempio di recente per scoprire eventuali anomalie presenti nelle piattaforme che trattano le “criptovalute” (che sono notoriamente prive di controllo istituzionale) oppure per individuare la presenza di “visualizzazioni” generate fraudolentemente da “social bot” per gonfiare i profili social alla ricerca di sponsor pubblicitari.

La Benford fu anche protagonista per la scoperta della vergognosa truffa legata alla formazione del tasso interbancario “Libor” a Londra (cfr. Tracking the Libor Rate: Rosa M. Abrantes – Metz and Sofia B. Villas-Boas, New York University Luglio 2010) e da ultimo, purtroppo anche sui dati Covid.

 

5. Spiegazione del fenomeno

 

La domanda fondamentale è: perché accade tutto questo? La risposta, che si propone in questo documento, è volta a favorire una comprensione semplice ed intuitiva, lasciando le considerazioni più complesse ed approfondite ai trattati di matematica.

Allo stato attuale i fondamenti scientifici di analisi numerica su cui si fonda tutta la materia si riassumono negli studi del prof. Ted  Hill  che insieme al prof. Berger ha recentemente pubblicato un libro allo scopo di fare una sintesi sul livello di conoscenza raggiunto: An introduction to Benford’s Law, Princeton ed., 2015; di rilevante interesse scientifico è anche la pubblicazione del Prof. Kossovsky della New York University “Benford’s Law”, ed. World Scientific, 2014. In generale la letteratura sull’argomento è cospicua ed è tutta raccolta sul sito  www.benfordonline.net.

Tornando alla dimostrazione intuitiva si immagini un insieme di numeri reali scelti casualmente nell’intervallo compreso tra: 1 e 10 e partendo dalla banale considerazione che: tutti i numeri compresi tra 1 e 1,999 iniziano per 1, tutti i numeri compresi tra 2 e 2,999 iniziano per 2, tutti i numeri compresi tra 3 e 3,999 iniziano per 3 e così via…, si giunge facilmente a stabilire che:

nel primo intervallo (1-1,999) il rapporto tra il maggiore: 1,999 e il minore: 1 è 1,999;

nel secondo intervallo (2-2,999) il rapporto è di circa 2,999/2 = 1,5;

nel terzo intervallo (3-3,999) il rapporto è circa 3,999/3 = 1,33

e così via a scendere fino al 10.

I rapporti danno luogo ad una serie di valori via via sempre più bassi (2> 1,5> 1,33…) e la decrescita è molto veloce. Quindi, c’è molto più “spazio” per un numero compreso nell’intervallo 1-1,999 (che inizia per 1) che per un numero compreso nell’intervallo 9-9,999 (che inizia per 9). Vi è quindi molta più probabilità di trovare un numero che inizia per 1 piuttosto che un numero che inizia per 9 nell’insieme dei numeri reali compreso nell’intervallo: 1-10.

Un altro esempio, ancora più semplice lo si trova osservando la serie di numeri naturali tra 1 e 20: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, i numeri che iniziano per 1 sono più della metà (11) e solo due iniziano con la cifra 2, se continuiamo ad aggiungere numeri fino arrivare a 200 e poi a 2000, e così via scopriremo che i numeri con 1 iniziale saranno sempre maggiori di quelli con il 2 che saranno maggiori di quelli che iniziano con il 3 ecc..

Come vedremo questo fenomeno numerico non si trova in qualsiasi serie di dati ma è assai frequente in quelle che misurano fenomeni economici e finanziari tipicamente originati da combinazioni lineari casuali. Un esempio classico (tra i tanti in questo ambito) è rappresentato dalla serie numeriche rappresentativa dei ricavi giornalieri di un’azienda il cui risultato finale è dato dalla sommatoria di tutte le singole operazioni di vendita dei singoli articoli ottenuti dalla combinazione moltiplicativa: P x Q, (prezzo per quantità).

Normalmente le vendite non sono condizionate da una predeterminazione fissata tra le parti (come accade per esempio nei contratti di somministrazione periodica di beni / servizi giornalieri) ma dipende dall’incontro spontaneo di domanda e dell’offerta che di fatto è la combinazione di una serie di fattori interni ed esterni che si intrecciano tra loro in modo del tutto casuale ed imprevedibile.

Se, per effetto di errori o frodi, nei sistemi contabili vengono rilevate, in maniera sufficientemente reiterata, grandezze numeriche non corrispondenti a reali transazioni economiche, il sopracitato processo di combinazione lineare casuale viene ad essere interrotto, pertanto si allontanerà dalla distribuzione prevista da Benford.

Se tale scostamento supera una determinata soglia, più o meno alta in funzione del livello di errore ritenuto accettabile, lo scostamento stesso sarà ritenuto rilevante, dal punto di vista statistico, in misura tale da essere considerato un dato anomalo (red flag) che in quanto tale necessita di una spiegazione.

Questa conclusione arriva basandosi sulla constatazione che le azioni umane non riproducono la casualità, gli individui scelgono i numeri secondo la loro convenienza o secondo preferenze psicologiche; si veda a riguardo T. Hill, The difficulty of faking data, in Change, 12(3): 27-31, 1999.

Pertanto, i numeri inventati da coloro che commettono frodi od errori rilevando inesistenti beni o servizi scambiati non saranno, molto probabilmente, conformi alla Legge di Benford. Il primo studioso, come già anticipato, che si è occupato delle applicazioni della Legge di Benford in ambito contabile e forense è stato il Prof. Mark Nigrini, che ha di recente pubblicato due volumi teorico-pratici: Benford’s law, 2012 e Forensic Analitycs, 2011 entrambi ed. Wiley & Sons, anche la dottrina contabile americana si è occupata della materia, tra i tanti si rinvia a The Effective use of Benford’s Law…, Durtschi, Hillison, Pacini 2004 in Journal of Forensic Accaunting.  

Si segnalano inoltre anche i manuali operativi Financial Forensic, Dorrell & Gadawsky, Ed. Wiley, e Using analitics to detect possible fraud, Pamela Mantone ed. Wiley & sons.

In Italia la Legge di Benford assume ufficialmente il ruolo di utile strumento di contrasto delle frodi aziendali con l’introduzione dei Principi di Revisione internazionali (ISA). Il suo specifico utilizzo è indicato nella Guida all’utilizzo dei principi di revisione internazionali nella revisione contabile delle P.M.I., volume I (tabella: 10.5-4) pubblicato dal Consiglio Nazionale Dottori Commercialisti ed Esperti Contabili.

Rientra perfettamente nei protocolli di lavoro della revisione, ma purtroppo la quasi totalità dei revisori in Italia ne ignora la natura. Negli Stati Uniti la possibilità di utilizzare tale strumento per l’attività di contabilità forense al fine di misurare l’analisi dell’attendibilità dei dati contabili rappresentati nei bilanci o nei report finanziari, è diffusa da tempo grazie al lavoro del citato Prof. Nigrini che si occupa prevalentemente dell’applicazione della legge di Benford, quale strumento analitico di verifica dei dati contabili finalizzato all’individuazione di valori potenzialmente manipolati in quanto significativamente non conformi allo schema benfordiano.

 

6. Condizioni applicative e proprietà

Innanzitutto, quando ed in quali condizioni i dati dovrebbero conformarsi alla legge di Benford? Tale conformità non vale per tutte le serie numeriche. Nigrini ci fornisce un elenco completo delle condizioni preliminari:

1. i numeri devono rappresentare fatti o comunque eventi, per esempio: l’ammontare delle vendite o degli acquisti giornalieri oppure il volume di azioni scambiate...;
2. non ci devono essere limitazioni precostituite in tali elenchi sia nei valori minimi che nei valori massimi (per esempio nelle somministrazioni pre concordate);
3. non devono essere numeri utilizzati come numeri identificativi: numeri di serie, numeri di partite iva, numeri di licenze o numeri telefonici…;
4. una serie è solitamente conforme se è costituita per la maggior parte da numeri di “dimensione” minore rispetto ai valori di maggiori dimensioni. Inoltre, l’ordine di grandezza che differenzia i numeri di maggiore entità risulta nettamente più alto dell’ordine di grandezza che differenzia i valori di minore “dimensione”; ciò che si evidenzia nel fatto che normalmente la media aritmetica della serie risulta essere superiore alla mediana;
5. l’emersione delle evidenze numeriche che provano la conformità della serie alla Legge Benford si manifesta palesemente in presenza di numerose quantità di dati; con un set di numeri più piccolo si rende necessario utilizzare, come si vedrà, ulteriori tecniche;
6. l’ordine di grandezza, che spazia tra il numero più piccolo ed il numero più grande, deve essere superiore di uno o due ordini di grandezza (condizione molto frequente nei dati economici e finanziari).

Le serie numeriche conformi alla Legge di Benford, godono della proprietà dell’“invarianza di scala” secondo cui, moltiplicando tutti i numeri per una costante, si determina una nuova serie che gode anch’essa della distribuzione delle prime cifre conformi alla legge di Benford.

 

7. Come misurare il livello di “conformità” alla Legge di Benford

Nigrini suggerisce di utilizzare la “Media delle deviazioni assolute” (M.A.D.) come valore che al superamento di determinate soglie critiche, variabili in funzione al numero di prime cifre preso in considerazione, segnala la mancata conformità alla distribuzione di frequenza delle prime cifre prevista da Benford e di conseguenza sia espressione di potenziali errori o frodi contabili.

La formula è la seguente:

 

                                   ∑ | AP - EP |

            M.A.D:   ----------------------------                    ( 2 )

                                                K

ove:

AP il valore della frequenza effettivamente rilevata espressa in valore decimale;

EP il valore della frequenza attesa, espressa in valore decimale, secondo Benford in base all’equazione logaritmica (1); 

K è il numero possibile di cifre 9 per la singola cifra, o 90 per le prime due cifre e così via. L’operatore matematico al numeratore: |  | (valore assoluto) conduce sempre ad una deviazione positiva indipendentemente dal segno della differenza algebrica. Le soglie critiche per la prima cifra, stabilite empiricamente in maniera restrittiva, sono le seguenti:

                        da 0,000 a 0,006 strettamente conforme

                        da 0,006 a 0,012 conformità accettabile

                        da 0,012 a 0,015 scarsamente conforme

                        oltre 0,015 totalmente non conforme      

Naturalmente la formula (2) non tiene conto del numero dei dati analizzati ed è quindi possibile che rilevanti deviazioni medie non siano “significative” (dal punto di vista statistico), vi è quindi la necessità di eseguire adeguati test statistici allo scopo di quantificarne il livello di significatività.

 

8. Interpretazione dei risultati con Test Statistici

Vi sono due fondamentali concetti da tener presente nell’adozione del procedimento di analisi digitale basato sulla legge di Benford:

1. l’efficacia di questa analisi dipende dal livello dei dati manipolati che si trovano nella serie numerica.
2. la mancata conformità non significa necessariamente che i dati contabili contengano errori o frodi.

La domanda di fondo da porsi è: a quale livello la deviazione tra valori effettivi osservati ed attesi è sufficientemente larga da essere considerata “significativa”?

 

Un utile test riferito ad ogni possibile cifra analizzata:

Z - Statistico

 

                                     | AP - EP | - (1 / 2N)

                        Z =      __________________________ (3)

                       

                                               √ EP (1- EP)/ N         

Per ciascuna osservazione si determina il valore assoluto dello scarto tra valore effettivo e valore atteso: | AP-EP | il fattore di correzione: 1/2N è utilizzato solo quando è più piccolo del valore assoluto; il tutto viene rapportato alla radice quadrata del valore atteso diviso per il numero complessivo dei dati osservati N.

La struttura della formula porta come conseguenza che anche un significativo scarto tra valori osservati ed attesi in presenza di un numero di osservazioni più ristretto potrebbe essere risultare non “significativo”, a meno di ridurre l’intervallo di confidenza (pari al 95%) accettando quindi un errore maggiore del 5% con il rischio di individuare: “falsi positivi” intesi come rilevazioni che solo apparentemente sembrano essere la risultante di frodi od errori, nel nostro caso non si accetta di superare la soglia di errore del 5%.

Un altro importante test Statistico, che coinvolge tutto il campione di dati è il :

                  2

  “Chi” Quadrato: X

 

  2           k                                 

 X = N * ∑  ( APi – EPi )2 / EPi   

               i = 1             

Ove N è il numero del campione di dati esaminato.

K è il numero delle cifre sotto osservazione (1<k<9) per la singola cifra oppure (10<k<99) nel caso delle prime due cifre; tale test prescinde dal numero dei dati analizzati.

Per esempio: nel caso delle prime due cifre, la soglia al di sotto della quale la cosiddetta “ipotesi nulla”, quando (APi - EPi) tende a zero si verifica, con un livello di errore non superiore del 5%, è pari a 112,02. Per valori superiori a tale limite, sempre nel caso delle prime due cifre, vale l’ipotesi “alternativa”: ovvero serie non conforme, ritenendo tale conclusione statisticamente valida con un margine d’errore inferiore del 5%.

 

9. Difficoltà operative

Un aspetto critico, nei bilanci, nasce dal fatto che dovendo effettuare “un’analisi esterna”, ovvero un’analisi posta in essere su bilanci o reports pubblici, l’analista stesso dispone di un set relativamente limitato di dati. Tuttavia, il rischio di rilevare la presenza di “falsi positivi”, quindi di segnalare la presenza di bilanci manipolatati quando in realtà non lo sono è circoscritto dall’utilizzo dell’indice Chi Quadrato, sulla prima cifra (quindi con 8 gradi di libertà pari a 9 = numero delle prime cifre - 1) con un margine di errore non superiore al 5%.

Infatti, la Legge di Benford è “affamata di numeri” e dà il meglio di sé in presenza di un largo set di dati. Per mitigare questa limitazione in presenza di dati di bilancio, la tecnica operativa offre però ingegnose soluzioni pratiche.

Un altro discorso, un po’ più delicato, si apre di fronte all’obiezione che essendo ormai nota la dinamica di Benford i potenziali manipolatori potrebbero (con grosse difficoltà) raggiungere i loro scopi lasciando inalterata la frequenza distributiva. Anche qui i recenti sviluppi della ricerca hanno già trovato le opportune soluzioni di contrasto.

 

10. Prospettive future

La Legge è stata scoperta circa 80 anni fa ma riserva ancora molti lati oscuri e le ricerche in campo matematico sono ancora in corso. Un grande contributo alla circolazione delle idee e delle ricerche è arrivato lo scorso anno dal Congresso Internazionale promosso dall’Istituto di Ricerca dell’Unione Europea, che ha visto finalmente l’Italia protagonista, a Stresa (Benford’s Law Conference, 10-12 Luglio 2019).

In questo importante appuntamento si sono confrontati tutti i maggiori esperti in materia di diverse Università italiane e straniere ed esponenti di Autorità ed Agenzie fiscali italiane ed europee.

Nel trattare grosse quantità di dati la Legge di Benford permette di superare agevolmente le limitazioni delle campionature, naturalmente i segnali di anomalie riscontrati (red flags) andranno opportunamente valutati con spirito critico, occorre infatti trovare il motivo delle anomalie, specialmente se di elevata ampiezza.

 

11. Conclusioni

La legge di Benford rappresenta uno strumento straordinario non solo nel campo forense e della revisione, le tecniche che ho sopra illustrato rappresentano il livello più noto e semplice (primary level).

Le ricerche più recenti hanno trovato nuove e più sofisticate “proprietà” (tra tutti cfr. Kossowsky op. citata) che ci permettono di allungare lo sguardo ancora di più, oltre l’orizzonte delle verità apparenti.